Oh boy...

I was recently reading a very informative Guitar Player magazine article on triads, discussing the use of triads as the basis for melodic soloing. Although I personally didn’t love the musical example, it certainly demonstrated the idea quite effectively. But I also noticed a shortcoming to this kind of information overload, one that I have been quite guilty of myself.

The article, much like this blog, is geared more towards the idea of improvisation. Yet, so far my experience in the past 3 weeks has been that the sophistication in the lines I’m discovering has yet to rub off very much on the kinds of things I’m improvising. Interestingly enough, the new triad shapes that are appearing in my playing, albeit in a simpler way and using less of them than when I write a line, are resulting more from the line building than the exercises. The exercises don’t seem to be as helpful so far. Although I know they will be eventually. But still, when I sit down to write, I come up with things that are far beyond my powers of instant computation.

Here’s an example from a solo for an original piece I’ve started working on:

Now I can play some of these lines in the solo, I can create tiny variations on them, but I’m not spinning off ideas that use the same concepts just yet. Why not?

Writing solos like this is a great process, and as I mentioned, writing lines has been more instantly gratifying in terms of applying ideas to my playing than waiting for the seeds being planted by the exercises to grow and bloom. But taking the long view, what I need is more exercises, more mechanical patterns to work through that will allow me to systematically explore all the possibilities which these concepts imply, taking these ideas beyond preconceived licks and allowing a more free application of these advanced textures while improvising.

So, in the last article, I put out four lines and then talked about what made each one special, and now I’m going to create a mechanical exercise based on what was cool about each one.

1. Alternating between ascending, descending, and broken. There are a massive number of combinations using these 3 interchangeable patterns, especially when there are 4 “broken” (mixture of the first 2) patterns. It might also be wise to start by interchanging only two patterns before moving on to 3. That’s a lot of work for 7 positions in two different scales (I’ll save harmonic minor for the next lifetime thank you).

Since this stuff is so complicated we won’t take anything for granted. This means there are 36 combinations of A,D,B1,B2,B3, and B4 including AA, DD, B1B1, etc. They are all pretty complicated and need to be investigated independently. Perhaps the smartest place to start would be going through all the doubles AA, DD, B1B1, B2B2, B3B3, and B4B4 to get a better feel for all of them before starting to mix them up.

And at this point, if there still seems to be a reason to investigate combinations of 3 as compulsively (although maybe that time if anybody makes it that far there won’t be a point to them anyways), there should be 216 different ways to play combinations of these patterns. Of course all this is really just a third of the work because you can start on Am/C and F/C, plus of course the other 13 positions of the major and melodic minor scales.

1. Using Passing Tones between chord tones. Just to keep the math at a point where this might take less than 20 years once it’s all added up, how about limiting ourselves to the combination of only two parameters at a time. Passing tones can either be between 1 and 3, 3 and 5, and then there are 3 possibilities to get from 5 back to 1 (play both or only one of them)

We have a name for when all the chord tones are connected by passing tones already: the scale.

Now here’s where our understanding of inversions and ability not to get lost in the material is tested to the extreme. I think anybody’s first instinct would be to simply put a passing tone on the first interval:

But we’ve already broken our rule of not combining more than 2 parameters. Let’s try and put a passing tone in between the same chord tones regardless of the inversion.

Yikes! We ran into a problem pretty fast. What to do now? There is no passing tone. Well, perhaps we can just skip the passing tone when it isn’t there and see what kind of funky rhythmic displacement this will create (clue: 11 note cycle won’t meet up with 4 until 44)

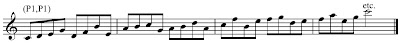
No matter what combination of passing tones you pick, there will always be this problem (when trying to create a mechanical or cyclical exercise)

This starts getting pretty weird as an exercise, but that 3rd bar is pretty cool. Maybe now we could create an intervallic sequence that isn’t necessarily triadic based on the 3rd bar?

And now that we’ve left our whole first constraint from the very first article (briefly) of basing everything on triads, couldn’t we abandon our other constraint and play this pattern in another cycle? (crap!!!! couldn’t that apply to everything we’ve talked about!?)

3.Using common tones as pivots between triads. Well obviously this one won’t work in cycle 2(/7), and cycle 3/6 just turns into a 4 note arpeggio, which isn’t exactly new to anybody anyways, so let’s look at cycle 4/5, which is so much fun because there is only one common tone. Now, in the name of keeping our goal of creating mechanical brainteasers, we’re going to imbed one cycle within another. In other words we’re going to do pairs of cycle 4, moving up in cycle 2. The pattern is 3 beats long. If you play it a couple of times you’ll see what I mean. This kind of larger sequence of imbedded patterns is a neat idea which I was first introduced to in Dave Liebman’s Chromatic Approach to Jazz Harmony. Liebman talks about using exact intervallic relationships, whereas this is looking at things from a more diatonic perspective. I’m really not sure which is harder, and I think the answer might depend on the instrument being used as well.

Another possibility, since the pattern seems to start and end on the same note, is to eliminate the repetition.

Here something interesting has happened. It turns out something much simpler is happening than what we set out to do(think of it as simplifying an equation).

Let’s go back to cycle 7 now and see what we can come up with.

And now there’s a million different ways to go about playing any/all/none of this stuff but one thing is for sure and it’s that there sure are a lot of ways to navigate through a diatonic scale.